Motivation

Given a set of $n$ points $P$ on a real line and a query interval $[x:x’]$ find all the points inside the interval.

Construct a binary search tree from $P$ and perform the following query:

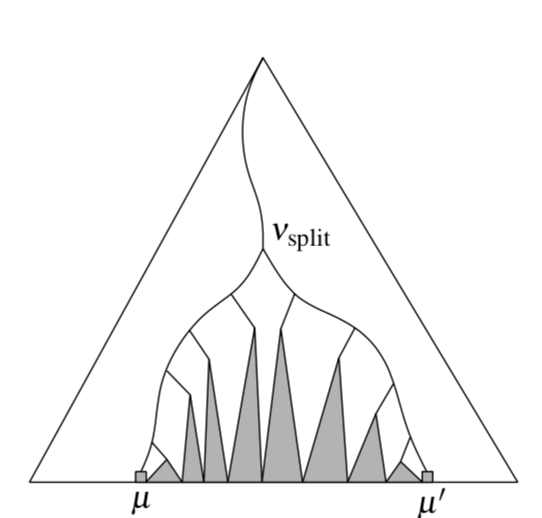
Figure: Example of searching in range tree

• Search for $x$ and $x’$ until we get to $v_{\rm split}$ where the search path splits.
• From the left child of $v_{\rm split}$ we continue search with $x$ and at every node $v$ we where search path goes left we all points in right subtree of $v$.
• Symmetrically we go right from $v_{\rm split}$ searching for $x’$ and taking left subtrees of $v$ respectively.

Definition

Canonical Subset of node $v$ (i.e. $P(v)$): subset of points stored in the leaves of the subtree at $v$.

2-D Range Trees

• The main tree is a balanced binary search tree built $T$ built on the x-coordinates of $P$.
• For any internal node / leaf node $v$ in $T$, the canonical subset $P(v)$ is stored in a balanced binary search tree $T_1(v)$ on the y-coordinates of the points. The node $v$ contains a pointer to the root of $T_1(v)$.

Creation $O(n\log n)$

Note Use presorted $P$

• Create $T_1(v)$ binary search tree.
• If $P$ has only one point then create leaf else split $P$ into two sets $P_{\rm left}$ and $P_{\rm right}$ using $x_{\rm mid}$ median point. Recursively create $v_{\rm left}$ and $v_{\rm right}$ from $P_{\rm left}$ and $P_{\rm right}$ respectively. Create a node with $x_{\rm mid}$ and $v_{\rm left}$ and $v_{\rm right}$ left and right children of this node. Make $T_1(v)$ the associated structure of $v$.

Querying $O(\log ^2n +k)$

• Find $v_{\rm split}$
• If $v_{\rm split}$ is a leaf check point inside it and report if necessary.
• Else
  • Follow path to $x$ and perform 1-D range query on the subtrees right of the path. Also check if point stored at the final leaf node $v$ must be reported.
  • Similary do for $x’$ and perform 1-D range query on the subtrees left of the path from $v_{\rm split}$. Again check at the end for the point stored at $v$.

Fractional Cascading

If two sets of objects $S_1$ and $S_2$ are stored int sorted arrays $A_1$ and $A_2$. To find keys in $[y:y’]$

• We can binary search for ceil of $y$ in $A_1$ and then walk along the array until the floor of $y’$. Similary for $S_2$. Total time will be $O(k)$ plus two binary searches ($k$ reported objects).
• If $S_2\subseteq S_1$ we can maintain pointers from $A_1$ to $A_2$, i.e. we store the pointer to ceil key for every value in $A_1$. This will avoid the second binary search.

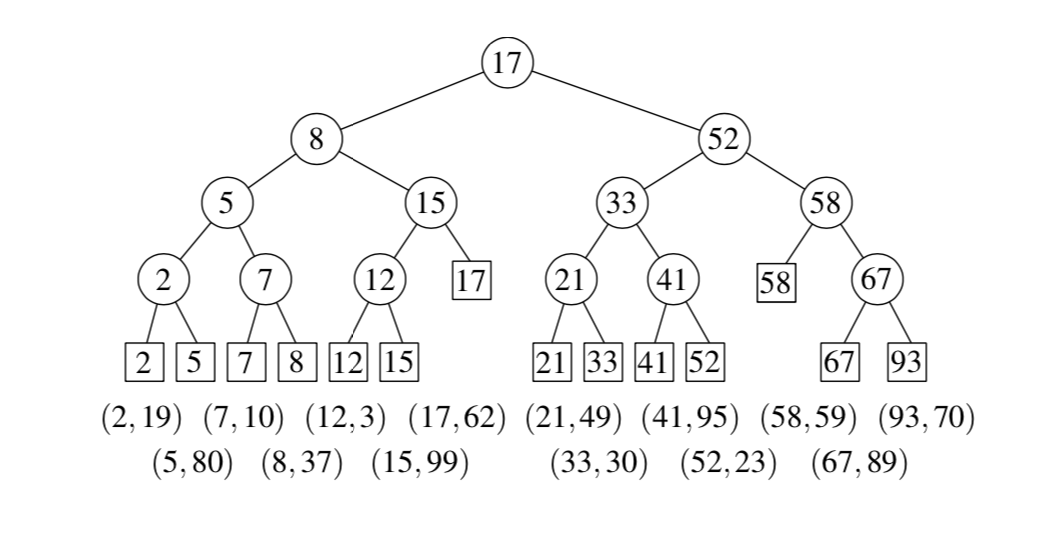
Figure: Layered Range Tree showing only x-coordinates. Full points are given below

Similarly $P(lc(v))\subseteq P(v)$ and $P(rc(v))\subseteq P(v)$. Instead of associated binary trees we will store an array sorted on the y-coordinates. Each value in the array will additionaly store two pointers to $A(lc(v))$ and $A(rc(v))$. This becomes the layered range tree. This makes the query time $O(\log n + k)$.

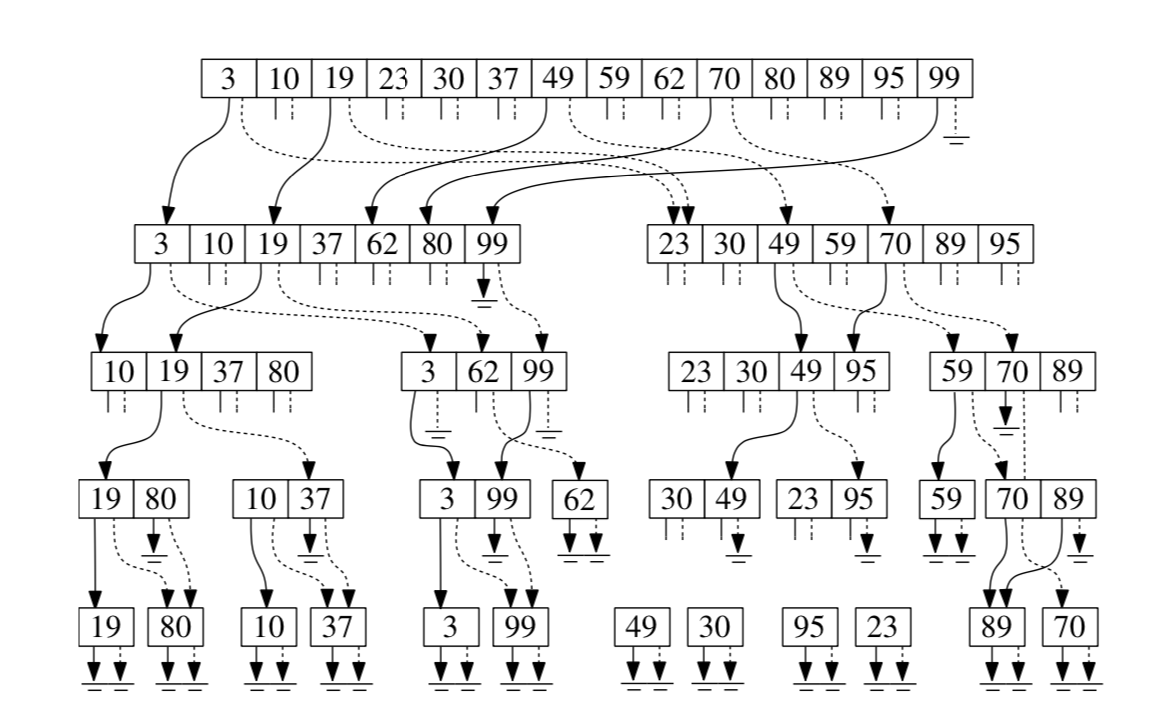
Figure: The associated arrays with the nodes.

While querying for $[x:x’]\times[y:y’]$:

• We search for $x$, $x’$ and $v_{\rm split}$. At $A(v_{\rm split})$ we we find the ceil entry of $y$.
• While searching in $x$ and $x’$ in main tree we keep track of ceil entry of $y$ by following pointers in constant time.